Три космические скорости
В первое время после запуска искусственного спутника Земли часто можно было слышать вопрос: "Почему спутник
 после выключения двигателей продолжает обращаться вокруг Земли, не падая на Землю?".
после выключения двигателей продолжает обращаться вокруг Земли, не падая на Землю?".
Так ли это? В действительности спутник "падает" – он притягивается к Земле под действием силы тяжести. Если бы не было притяжения, то спутник улетел бы по инерции от Земли в направлении приобретённой им скорости. Земной наблюдатель воспринял бы такое движение спутника как движение вверх. Как известно из курса физики, для движения по кругу радиуса R тело должно обладать центростремительным ускорением a=V2/R, где а – ускорение, V – скорость. Поскольку в данном случае роль центростремительного ускорения играет ускорение силы тяжести, то можно написать: g=V2/R. Отсюда нетрудно определить скорость Vкр, необходимую для кругового движения на расстоянии R от центра Земли: V12=gR. В приближённых расчётах принимается, что ускорение силы тяжести постоянно и равно 9,81 м/сек2.
Какова же та начальная скорость, которую нужно сообщить телу, чтобы оно двигалось вокруг Земли по окружности? Нам уже известно, что чем большую скорость сообщить телу, тем на большее расстояние оно улетит. Траектории полёта будут эллипсами (мы пренебрегаем влиянием сопротивления земной атмосферы и рассматриваем полёт тела в пустоте). При некоторой достаточно большой скорости тело не успеет упасть на Землю и, сделав полный оборот вокруг Земли, возвратится в начальную точку, чтобы вновь начать движение по окружности. Скорость спутника, движущегося по круговой орбите вблизи земной поверхности, называется первой космической скоростью и представляет собой ту скорость, которую нужно сообщить телу, чтобы оно стало спутником Земли. Первая космическая скорость у поверхности Земли может быть вычислена по приведенной выше формуле для скорости кругового движения, если подставить вместо R величину радиуса Земли (6400 км), а вместо g – ускорение свободного падения тела, равное 9,81 м/сек2. В результате найдём, что первая космическая скорость равна
V1=7,9 км/сек.
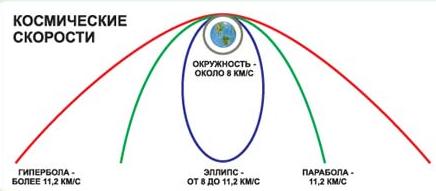
Под второй космической скоростью понимают скорость, необходимую для того, чтобы тело преодолело земное тяготение. Если тело достигнет второй космической скорости, то оно может удалиться от Земли на любое сколь угодно большое расстояние (предполагается, что на тело не будут действовать никакие другие силы, кроме сил земного тяготения).
Проще всего для получения величины второй космической скорости воспользоваться законом сохранения энергии. Совершенно очевидно, что после выключения двигателей сумма кинетической и потенциальной энергии ракеты должна оставаться постоянной. Пусть в момент выключения двигателей ракета находилась на расстоянии R от центра Земли и имела начальную скорость V (для простоты рассмотрим вертикальный полёт ракеты). Тогда по мере удаления ракеты от Земли скорость её будет уменьшаться. На некотором расстоянии rmax ракета остановится, так как её скорость обратится в ноль, и начнёт свободно падать на Землю. Если в начальный момент ракета обладала наибольшей кинетической энергией mV2/2, а потенциальная энергия была равна нулю, то в наивысшей точке, где скорость равна нулю, кинетическая энергия обращается в ноль, переходя целиком в потенциальную. Согласно закону сохранения энергии, находим:
mV2/2=fmM(1/R-1/rmax) или V2=2fM(1/R-1/rmax).
полагая rmax ,бесконечно, найдём значение второй космической скорости:
VII= 2fM/R = 2 fM/R = 2 VI .
Оказывается, она превышает первую космическую скорость в 2 раз. Если вспомнить, что ускорение свободного падения g=fM/R2, то приходим к формуле VII= 2gR . Чтобы определить вторую космическую скорость у поверхности Земли, следует в эту формулу подставить R=6400км, в результате чего получим:
VII =11,19 км/сек
По приведённым формулам можно вычислить параболическую скорость на любом расстоянии от Земли, а также определить её значение для других тел солнечной системы.
 Выведенная формула параболической скорости может быть использована и в приближённых расчётах межзвёздного полёта. Чтобы осуществить полёт к звёздам, необходимо преодолеть солнечное притяжение, т.е. Звездолёту должна быть сообщена скорость, при которой он будет двигаться относительно Солнца по параболической или гиперболической орбите. Назовём наименьшую начальную скорость третьей космической скоростью. Подставляя в формулу параболической скорости вместо М значение массы Солнца, а вместо R – среднее расстояние от Земли до Солнца, найдём, что звездолёту, стартующему с земной орбиты, должна быть сообщена скорость около 42,2 км/сек. Итак, если телу сообщить гелиоцентрическую скорость в 42,2 км/сек, то оно навсегда покинет солнечную систему, описав относительно Солнца параболическую орбиту. Выясним, какой должна быть величина скорости относительно Земли, чтобы обеспечить удаление тела не только от Земли, но и от Солнца? Иногда рассуждают так: поскольку средняя скорость Земли относительно Солнца равна 29,8 км/сек, то необходимо сообщить космическому кораблю скорость, равную 42,2 км/сек – 29,8 км/сек, т.е. 12,4 км/сек. Это неверно, так как в этом случае не учитывается движение Земли по орбите во время удаления космического корабля и притяжение со стороны Земли, пока корабль находится в сфере её действия. Поэтому третья космическая скорость относительно Земли больше 12,4 км/сек и равна
Выведенная формула параболической скорости может быть использована и в приближённых расчётах межзвёздного полёта. Чтобы осуществить полёт к звёздам, необходимо преодолеть солнечное притяжение, т.е. Звездолёту должна быть сообщена скорость, при которой он будет двигаться относительно Солнца по параболической или гиперболической орбите. Назовём наименьшую начальную скорость третьей космической скоростью. Подставляя в формулу параболической скорости вместо М значение массы Солнца, а вместо R – среднее расстояние от Земли до Солнца, найдём, что звездолёту, стартующему с земной орбиты, должна быть сообщена скорость около 42,2 км/сек. Итак, если телу сообщить гелиоцентрическую скорость в 42,2 км/сек, то оно навсегда покинет солнечную систему, описав относительно Солнца параболическую орбиту. Выясним, какой должна быть величина скорости относительно Земли, чтобы обеспечить удаление тела не только от Земли, но и от Солнца? Иногда рассуждают так: поскольку средняя скорость Земли относительно Солнца равна 29,8 км/сек, то необходимо сообщить космическому кораблю скорость, равную 42,2 км/сек – 29,8 км/сек, т.е. 12,4 км/сек. Это неверно, так как в этом случае не учитывается движение Земли по орбите во время удаления космического корабля и притяжение со стороны Земли, пока корабль находится в сфере её действия. Поэтому третья космическая скорость относительно Земли больше 12,4 км/сек и равна
VIII =16,7 км/сек.
Некоторые даты в истории космонавтики
| 4 октября 1957 года | Первый искусственный спутник Земли |
| 12 апреля 1961 года | Первый полет человека в космос (СРСР, Ю. Гагарин) |
|
|
|
|
|
|















